
Variables are all around us, but we rarely refer to them by name. Children might notice examples of variables when playing sports – for instance, scoring 3 now may change to 4 or 6 later!
It is the variables that enable them to double-bake recipes or track how many pages are left in a book.
Implicit knowledge of variables is already an extremely powerful skill for children to possess.
As they venture further into the field of mathematics, they get to understand that variables consist of symbols, and often letters. It helps in understanding the problems and finding solutions with changing values.
Are you a learner who wishes to understand the importance of variables among young learners? Then stay till the end of the article to understand the need for variables for young learners!
So, let’s get started!
Learning Variables for Kids
When children learn in math classes, they get instant, often visual results that help them understand how variables work. This opens up pathways to understanding the math behind variables.
This article’s purpose is to answer the following questions and give you all the essential knowledge for introducing variables to your students.
What Is a Variable?

One way of explaining variables to children is with real-world examples. When someone says there are three apples in a basket, everyone understands that this is an indicator of how many they should expect to find. Therefore, its number is three apples in a basket (the variable).
An illustrated lesson in variables involves adding one extra apple to an already full basket; when this fourth apple arrives, its number changes dramatically from three. From 3 apples at first, now 4 have joined it! Sometimes its exact figure remains unknown, but there will always be numbers involved!
Children learn a key concept about variables: you can refer to the amount of apples in a basket without knowing exactly how many there are in it.
Variables in Math
A child sits before a blackboard covered with algebraic variables written on it.
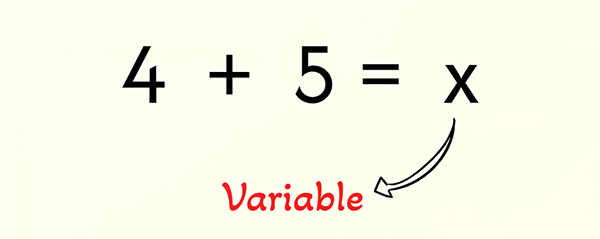
First time kids encounter variables is typically in mathematics class. Variables have two components – their value and name.
Variables may be introduced by asking students to solve for the value of an unknown variable, such as “x”. Pre-algebra math classes sometimes introduce variables by asking students to fill in blanks with different values of an x variable.
3 + 3 = _ The blank space here will eventually be filled in by an x.
3 + 3 = x
To help children learn the concept of variables as placeholders for unknown numeric values.
Later, children are introduced to the concepts of dependent variables and independent variables, as well as changing values for both. This allows graphs to illustrate how one variable’s value changes as adjustments are made to other variables.
This leads to an introduction of science for kids. They can participate in experiments where plant growth (the dependent variable) changes when you adjust sunlight exposure or water flow to it (the independent variable) over the course of an experiment.
Different Types of Variables
As we explore the vast world of variables, we encounter various varieties, each with its own set of properties and roles. There are dependent variables, independent variables, and constants – all helping create a more complete picture of mathematical reality.
Dependent Variables
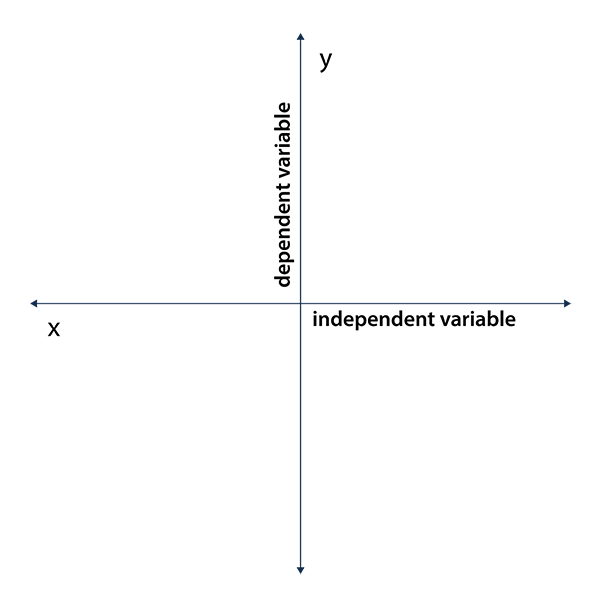
A dependent variable is any variable whose value changes based on another variable known as an independent variable, otherwise known as its “independent value”.
Think of it like this: one side goes up (independent variable), and the other goes down (dependent variable).
A mathematical equation typically uses this type of dependent variable as its output or result; for instance, in equation y = 3x + 2, “y” is considered the dependent variable since its value changes with each change to “x.”
Independent Variables
An independent variable refers to any variable that is altered or controlled in a scientific experiment or mathematical equation to test its effect on another variable – typically known as the dependent variable.
For example, when on a seesaw the side that moves by itself is considered independent since they don’t depend on each other for support or resistance from either end of the seesaw; similarly for equation y = 3x + 2, “x” stands in as independent.
Constants in Math
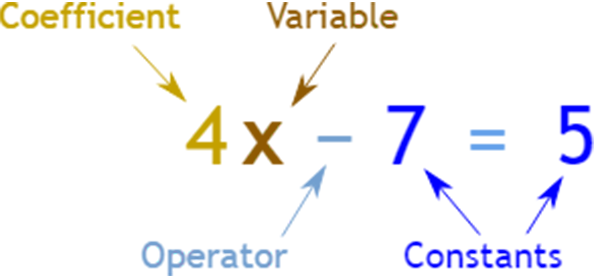
Constants provide stability by remaining constant over time. Contrasting with variables, which can represent various values at various times, constants remain the same throughout their existence.
For instance, in the equation y = 3x + 2, where 2 remains the same value regardless of what values are entered for x and y, using constants gives us more understanding into relationships among variables more easily.
Parts of Equation
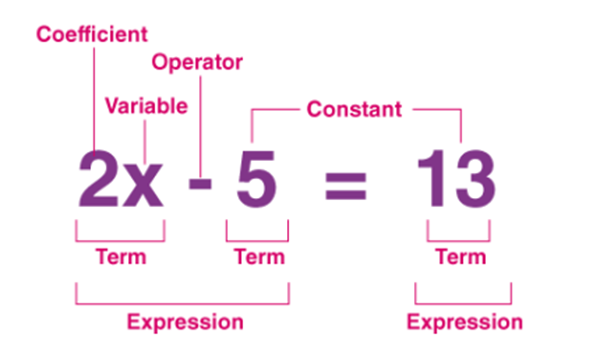
Mathematical equations contain many parts, each playing an essential part. There’s the left-hand side (LHS), right-hand side (RHS), variables, constants, coefficients (the numerical factor of a variable), operators (+, -, x, /), as well as operators (+/-x/y).
These all form part of an equation – for instance, in 3x + 2 = y both are LHSs while “y” forms part of RHS while x and “3x + 2 = y” are both variables. There, “3x + 2 =y”, variables while coefficient x (3/3 is the coefficient and constant of variable x and two operators (+/=) are operators involved – in 3x + 2=y].
Variable in Statistics
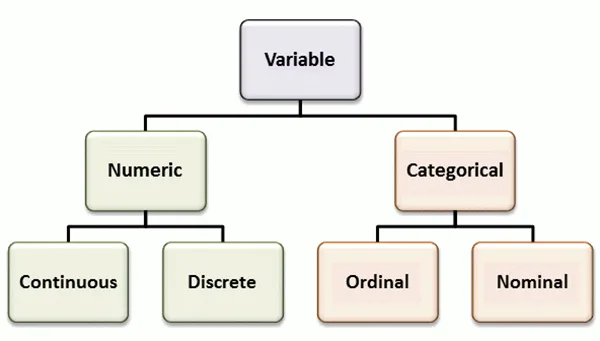
In statistics, variables hold an integral place. A variable can be defined as any attribute that describes someone, place, thing, or concept; its values can change from entity to entity.
Age, height, weight, and income can all serve as examples of variables used in statistics and used to gather, analyze, and interpret data before making informed decisions or predictions.
Categorical variables have categories and groups, and numerical ones expressed through numbers are the two primary types:
- Math Variables – There are multiple kinds of variables in math beyond dependent, independent, and constant ones; we will now take a look at them all:
- Discrete Variables: These variables have fixed values; for instance, students in a class can only ever be whole numbers.
- Continuous Variables: Continuous variables can take any value within their given range; for instance, height can take on any value within human dimensions.
- Random Variables: Random variables refer to variables with values determined by random events, such as dice rolling. A dice roll produces random variables whose potential outcomes could range anywhere between one and six, each having equal chances.
Bottom Line
By the time we’ve come to an end of our exploration of variables here on Brighterly, we hope that you have experienced just how powerful variables are as mathematical tools.
They allow us to express, explore, and solve a broad variety of mathematical issues by making math more accessible, abstract, universal and applicable in everyday situations.
The beauty of variables lies in their versatility – which makes math much more accessible!