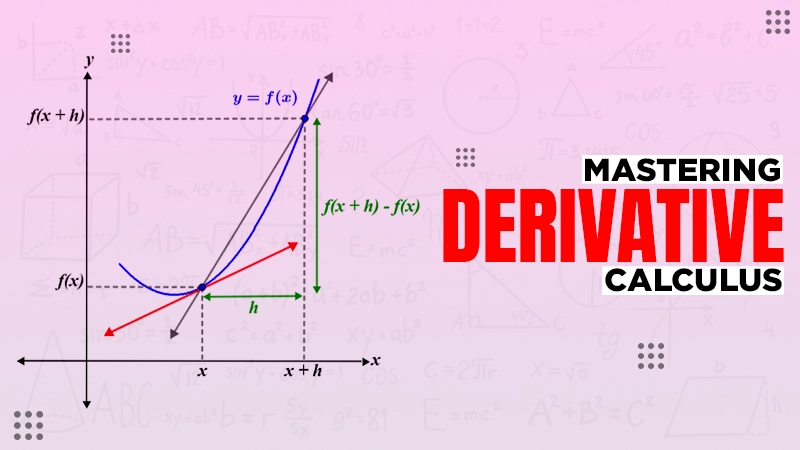
In calculus, the derivative is an essential kind that deals with the function’s derivatives with respect to a variable that is not dependent. This branch of calculus is very useful for determining the maximum and minimum values of any function.
It’s also useful for dealing with the solutions to differential equations. Mastering derivative calculus is necessary for students of mathematics and physics. In this post, we are going to explain derivative calculus in detail.
What is derivative calculus?
Derivative calculus is a fundamental branch of mathematics that is frequently used to measure the rate of change of a function with respect to non-dependent variables. The slope of the tangent line is also calculated with the help of this fundamental branch.
The differential of a function is denoted by f'(z) or d/dz f(z). It can be calculated using different methods, such as the limit definition, the power rule, the product rule, and the quotient rule. The formula used to find the derivative of a function using limit definition is:
t’(z) = limh→0 [(t(z + h) – t(z)) / h]
Rules of derivative calculus
Here are a few basic rules for taking the first derivative of the function:
| Name | Rule |
| Sum Rule: | d/dz [t(z) + h(z)] = d/dz [t(z)] + d/dz [h(z)] |
| Difference Rule: | d/dz [t(z) – h(z)] = d/dz [t(z)] – d/dz [h(z)] |
| Product Rule: | d/dz [t(z) * h(z)] = h(z) d/dz [t(z)] + t(z) d/dz [h(z)] |
| Constant Rule: | d/dz [K] = 0 |
| Constant function Rule: | d/dz [K t(z)] = K d/dz [t(z)] |
| Power Rule: | d/dz [t(z)]n = n [t(z)]n-1 d/dz [t(z)] |
| Quotient Rule: | d/dz [f(z) / h(z)] = 1/[h(z)]2 [h(z) d/dz (t(z)) – t(z) d/dz (h(z))] |
What is Advanced Differentiation?
The study of the differentials of the functions that are more complex than simple functions in calculus is said to be advanced differentiation. These functions may include implicit functions, parametric functions, vector-valued functions, and functions of several variables.
Some of the topics that are typically covered in advanced differentiation courses include:
- Implicit differentiation
- Partial differentiation
- Vector calculus
- Higher-order derivatives
Here are some examples of advanced differentiation concepts:
Implicit differentiation:
This is the process of differentiating an implicit function, which is an equation that defines y as a function of z but does not explicitly state y in terms of z. The derivative of y with respect to z is not considered a constant function.
In simple words, the derivative of the dependent variable with respect to the independent variable is said to be the implicit differentiation.
Partial differentiation:
This is the process of differentiating a function of several variables with respect to one of the variables while treating the other variables as constants. Such as consider a function t(u, v, w) will be differentiated as:
∂/∂u [t(u, v, w)], ∂/∂v [t(u, v, w)], or ∂/∂w [t(u, v, w)]
Vector calculus:
This is the study of calculus in the context of vector spaces. It is used to study the motion of objects in space, the flow of fluids, and other problems involving vectors.
Higher-order derivatives:
These are derivatives of derivatives. For example, the second derivative of a function is the derivative of its first derivative. The third derivative of a function is the derivative of the second derivative and so on.
Rules of Higher-Order Derivatives
For 2nd Order
Here are a few basic rules for taking the second-order derivatives of the function:
| Name | For 2nd order Derivative |
| Sum Rule: | d2/dz2 [t(z) + h(z)] = d2/dz2 [t(z)] + d2/dz2 [h(z)] |
| Difference Rule: | d2/dz2 [t(z) – h(z)] = d2/dz2 [t(z)] – d2/dz2 [h(z)] |
| Product Rule: | d2/dz2 [t(z) * h(z)] = h(z) d2/dz2 [t(z)] + 2[d/dz t(z) d/dz h(z)] + t(z) d2/dz2 [h(z)] |
| Constant Rule: | d2/dz2 [K] = 0 |
| Constant function Rule: | d2/dz2 [K t(z)] = K d2/dz2 [t(z)] |
| Power Rule: | d2/dz2 [t(z)]n = n (n – 1) [t(z)]n-2 |
For 3rd Order
Here are a few basic rules for taking the third-order derivatives of the function:
| Name | For 3rd Order Derivative |
| Sum Rule: | d3/dz3 [t(z) + h(z)] = d3/dz3 [t(z)] + d3/dz3 [h(z)] |
| Difference Rule: | d3/dz3 [t(z) – h(z)] = d3/dz3 [t(z)] – d3/dz3 [h(z)] |
| Product Rule: | d3/dz3 [t(z) * h(z)] = h(z) d3/dz3 [t(z)] + 3d2/dz2 [t(z)] d/dz [h(z)] + 3d/dz [t(z)] d2/dz2 [h(z)] + t(z) d3/dz3 [h(z)] |
| Constant Rule: | d3/dz3 [K] = 0 |
| Constant function Rule: | d3/dz3 [K t(z)] = K d3/dz3 [t(z)] |
| Power Rule: | d3/dz3 [t(z)]n = n (n – 1) (n – 2) [t(z)]n-3 |
Tips for Dealing with Advanced Differentiation
Solving advanced differentiation problems can be challenging, but it is possible with a solid understanding of the basics and a little practice. Here are some tips for solving advanced differentiation problems:
Understand the Basics
You need to have a sound knowledge and understanding of the basics of differentiation before dealing with advanced differentiation problems. You have a solid grip on the laws and methods for solving basic differentials.
Practice Regularly
Practicing regularly is the best way to solve advanced differentiation problems. Ask for help from your teachers and colleagues if you get stuck and solve a different variety of problems.
Use online Resources
There are many online resources available with instructional strategies that can help you learn about advanced differentiation and solve problems. Khan Academy, Paul’s Online Math Notes, and AllMath are just a few examples.
Don’t Give Up
Solving advanced differentiation problems can be challenging, but it is important to not give up. Keep practicing and asking for help until you master the concepts.
How to Solve Advanced Differentiation Problems?
Below are a few examples to learn how to solve advanced differentiation problems.
Example 1: For Implicit Differentiation
Differentiate 3zy – 4y2 + 2z = 2z2
Solution
Step 1: Apply the notation
d/dz [3zy – 4y2 + 2z] = d/dz [2z2]
Step 2: Apply the notation separately.
d/dz [3zy] – d/dz [4y2] + d/dz [2z] = d/dz [2z2]
Step 3: Take out constant terms.
3y d/dz [z] – 4d/dz [y2] + 2d/dz [z] = 2d/dz [z2]
Step 4: Differentiate the above terms.
3y [z1-1] – 4 [2 y2-1 d/dz [y]] + 2 [z1-1] = 2 [2 z2-1]
3y [z0] – 4 [2 y1 d/dz [y]] + 2 [z0] = 2 [2 z1]
3y [1] – 4 [2 y d/dz [y]] + 2 [1] = 2 [2 z]
3y – 8y dy/dz + 2 = 4z
– 8y dy/dz = 4z – 3y – 2
dy/dz = 4z/-8y – 3y/-8y – 2/-8y
dy/dz = -z/2y + 3/8 + 1/4y
Example 2: For Partial Differentiation
Differentiate 5wv2y – 2yv3w – 3y2w with respect to “y & w”.
Solution
With respect to “y”
Step 1: Apply the notation
∂/∂y [f(v, w, y)] = ∂/∂y [5wv2y – 2yv3w – 3y2w]
Step 2: Apply the notation separately.
∂/∂y [5wv2y – 2yv3w – 3y2w] = ∂/∂y [5wv2y] – ∂/∂y [2yv3w] – ∂/∂y [3y2w]
Step 3: Take out constant terms.
∂/∂y [5wv2y – 2yv3w – 3y2w] = 5wv2 ∂/∂y [y] – 2v3w ∂/∂y [y] – 3w ∂/∂y [y2]
Step 4: Apply the differential
∂/∂y [5wv2y – 2yv3w – 3y2w] = 5wv2 [1] – 2v3w [1] – 3w [2y]
∂/∂y [5wv2y – 2yv3w – 3y2w] = 5wv2 – 2v3w – 6wy
With respect to “w”
Step 1: Apply the notation
∂/∂w [f(v, w, y)] = ∂/∂w [5wv2y – 2yv3w – 3y2w]
Step 2: Apply the notation separately.
∂/∂w [5wv2y – 2yv3w – 3y2w] = ∂/∂w [5wv2y] – ∂/∂w [2yv3w] – ∂/∂w [3y2w]
Step 3: Take out constant terms.
∂/∂w [5wv2y – 2yv3w – 3y2w] = 5v2y ∂/∂w [w] – 2yv3 ∂/∂w [w] – 3y2 ∂/∂w [w]
Step 4: Apply the differential
∂/∂w [5wv2y – 2yv3w – 3y2w] = 5v2y [1] – 2yv3 [1] – 3y2 [1]
∂/∂w [5wv2y – 2yv3w – 3y2w] = 5v2y – 2yv3 – 3y2
Example 3: For Higher Order Derivative
Find the 2nd & 3rd order derivatives of t(z) = 3z3 + 4z2 – 5z4 + z5 with respect to “z” if the first order derivative is: t’(z) = 9z2 + 8z – 20z3 + 5z4
Solution
For 2nd derivative
Step 1: First of all, take the given algebraic expression and then write the 1st derivative of that function.
t(z) = 3z3 + 4z2 – 5z4 + z5
t’(z) = 9z2 + 8z – 20z3 + 5z4
Step 2: Now apply the differential notation to the first derivative.
d/dz [t’(z)] = d/dz [9z2 + 8z – 20z3 + 5z4]
Step 3: Now apply the notation of differential separately to each term of the function using sum & difference laws and take out the constant terms.
d/dz [9z2 + 8z – 20z3 + 5z4] = d/dz [9z2] + d/dz [8z] – d/dz [20z3] + d/dz [5z4]
d/dz [9z2 + 8z – 20z3 + 5z4] = 9 d/dz [z2] + 8 d/dz [z] – 20 d/dz [z3] + 5 d/dz [z4]
Step 4: Now use the power rule to differentiate the above expression.
d/dz [9z2 + 8z – 20z3 + 5z4] = 9 [2 z2-1] + 8 [z1-1] – 20 [3 z3-1] + 5 [4 z4-1]
d/dz [9z2 + 8z – 20z3 + 5z4] = 9 [2 z1] + 8 [z0] – 20 [3 z2] + 5 [4 z3]
d/dz [9z2 + 8z – 20z3 + 5z4] = 9 [2 z] + 8 [1] – 20 [3 z2] + 5 [4 z3]
d/dz [9z2 + 8z – 20z3 + 5z4] = 18z + 8 – 60z2 + 20z3
Hence the second derivative of the given function is:
t’’(z) = 18z + 8 – 60z2 + 20z3
For 3rd derivative
Step 1: First of all, take the given algebraic expression and then write the 2nd derivative of that function.
h(u) = 5u4 – 6u3 + 15u2 – (2u2 x 3u3)
t’’(z) = 18z + 8 – 60z2 + 20z3
Step 2: Now apply the differential notation to the 3rd derivative.
d/dz [t’’(z)] = d/dz [18z + 8 – 60z2 + 20z3]
Step 3: Now apply the notation of differential separately to each term of the function using sum & difference laws and take out the constant terms.
d/dz [18z + 8 – 60z2 + 20z3] = d/dz [18z] + d/dz [8] – d/dz [60z2] + d/dz [20z3]
d/dz [18z + 8 – 60z2 + 20z3] = 18 d/dz [z] + d/dz [8] – 60 d/dz [z2] + 20 d/dz [z3]
Step 4: Now use the power rule to differentiate the above expression.
d/dz [18z + 8 – 60z2 + 20z3] = 18 [z1-1] + [0] – 60 [2 z2-1] + 20 [3 z3-1]
d/dz [18z + 8 – 60z2 + 20z3] = 18 [z0] + [0] – 60 [2 z1] + 20 [3 z2]
d/dz [18z + 8 – 60z2 + 20z3] = 18 [1] – 60 [2 z] + 20 [3 z2]
d/dz [18z + 8 – 60z2 + 20z3] = 18 – 120z + 60z2
Hence the third derivative of the given function is:
t’’’(z) = 18 – 120z + 60z2
Conclusion
Now you can seek guidance on the basics and advanced differentiation from this post. We have discussed advanced differentiation along with solved examples to understand the concept accurately.